Computing is the next frontier for information theory. Intellectually, the goal of coded computing has been of interest from the days of von Neumann and Shannon. von Neumann examined this issue in his 1956 paper “Probabilistic Logics and the Synthesis of Reliable Organisms From Unreliable Components,” which was in turn motivated intellectually by Shannon’s 1948 paper, and by the application of understanding reliability of seemingly noisy biological systems. While the original biological application remains ill-understood, the recent increasing use of decentralized and distributed computing architectures, as well as increasingly noisy technologies at a device level, have motivated a resurgence of interest in the problem.

Coded computing is an effective technique to mitigate “stragglers” in large-scale and distributed matrix multiplication. In particular, univariate polynomial codes have been shown to be effective in straggler mitigation by making the computation time depend only on the fastest workers. However, these schemes completely ignore the work done by the straggling workers resulting in a waste of computational resources. To reduce the amount of work left unfinished at workers, one can further decompose the matrix multiplication task into smaller sub-tasks, and assign multiple sub-tasks to each worker, possibly heterogeneously, to better fit their particular storage and computation capacities. In this work, we propose a novel family of bivariate polynomial codes to efficiently exploit the work carried out by straggling workers. We show that bivariate polynomial codes bring significant advantages in terms of upload communication costs and storage efficiency, measured in terms of the number of sub-tasks that can be computed per worker. We propose two bivariate polynomial coding schemes. The first one exploits the fact that bivariate interpolation is always possible on a rectangular grid of evaluation points. We obtain such points at the cost of adding some redundant computations. For the second scheme, we relax the decoding constraints and require decodability for almost all choices of the evaluation points. We present interpolation sets satisfying such decodability conditions for certain storage configurations of workers. Our numerical results show that bivariate polynomial coding considerably reduces the average computation time of distributed matrix multiplication. We believe this work opens up a new class of previously unexplored coding schemes for efficient coded distributed computation.

In this work, we consider a sequence of $J$ matrix multiplication jobs which needs to be distributed by a master across multiple worker nodes. For $i\in \{1,2,\ldots,J\}$ , job- $i$ begins in round- $i$ and has to be completed by round- $(i+T)$ . In order to provide resiliency against slow workers (stragglers), previous works focus on coding across workers, which is the special case of $T=0$ . We propose here two schemes with $T > 0$ , which allow for coding across workers as well as the dimension of time. Our first scheme is a modification of the polynomial coding scheme introduced by Yu et al. and places no assumptions on the straggler model. Exploitation of the temporal dimension helps the scheme handle a larger set of straggler patterns than the polynomial coding scheme, for a given computational load per worker per round. The second scheme assumes a particular straggler model to further improve performance (in terms of encoding/decoding complexity). We develop theoretical results establishing (i) optimality of our proposed schemes for certain classes of straggler patterns and (ii) improved performance for the case of i.i.d. stragglers. These are further validated by experiments, where we implement our schemes to train neural networks.

We study coded distributed matrix multiplication from an approximate recovery viewpoint. We consider a system of $P$ computation nodes where each node stores $1/m$ of each multiplicand via linear encoding. Our main result shows that the matrix product can be recovered with $\epsilon $ relative error from any $m$ of the $P$ nodes for any $\epsilon > 0$ . We obtain this result through a careful specialization of MatDot codes — a class of matrix multiplication codes previously developed in the context of exact recovery ( $\epsilon =0$ ). Since prior results showed that MatDot codes achieve the best exact recovery threshold for a class of linear coding schemes, our result shows that allowing for mild approximations leads to a system that is nearly twice as efficient as exact reconstruction. For Entangled-Poly codes — which are generalizations of MatDot codes — we show that approximation reduces the recovery threshold from $p^{2} q + q -1$ to $p^{2}q$ , when the input matrices A, B are split respectively in to a $p \times q$ and $q \times p$ grids of equal-sized submatrices.

Gradient codes use data replication to mitigate the effect of straggling machines in distributed machine learning. Approximate gradient codes consider codes where the data replication factor is too low to recover the full gradient exactly. Our work is motivated by the challenge of designing approximate gradient codes that simultaneously work well in both the adversarial and random straggler models. We introduce novel approximate gradient codes based on expander graphs. We analyze the decoding error both for random and adversarial stragglers, when optimal decoding coefficients are used. With random stragglers, our codes achieve an error to the gradient that decays exponentially in the replication factor. With adversarial stragglers, the error is smaller than any existing code with similar performance in the random setting. We prove convergence bounds in both settings for coded gradient descent under standard assumptions. With random stragglers, our convergence rate improves upon rates obtained via black-box approaches. With adversarial stragglers, we show that gradient descent converges down to a noise floor that scales linearly with the adversarial error to the gradient. We demonstrate empirically that our codes achieve near-optimal error with random stragglers and converge faster than algorithms that do not use optimal decoding coefficients.

We consider the problem of coded computing, where a computational task is performed in a distributed fashion in the presence of adversarial workers. We propose techniques to break the adversarial toleration threshold barrier previously known in coded computing. More specifically, we leverage list-decoding techniques for folded Reed-Solomon codes and propose novel algorithms to recover the correct codeword using side information. In the coded computing setting, we show how the master node can perform certain carefully designed extra computations to obtain the side information. The workload of computing this side information is negligible compared to the computations done by each worker. This side information is then utilized to prune the output of the list decoder and uniquely recover the true outcome. We further propose folded Lagrange coded computing (FLCC) to incorporate the developed techniques into a specific coded computing setting. Our results show that FLCC outperforms LCC by breaking the barrier on the number of adversaries that can be tolerated. In particular, the corresponding threshold in FLCC is improved by a factor of two asymptotically compared to that of LCC.

We consider the problem of coded distributed computing where a large linear computational job, such as a matrix multiplication, is divided into $k$ smaller tasks, encoded using an $(n,k)$ linear code, and performed over $n$ distributed nodes. The goal is to reduce the average execution time of the computational job. We provide a connection between the problem of characterizing the average execution time of a coded distributed computing system and the problem of analyzing the error probability of codes of length $n$ used over erasure channels. Accordingly, we present closed-form expressions for the execution time using binary random linear codes and the best execution time any linear-coded distributed computing system can achieve. It is also shown that there exist good binary linear codes that not only attain (asymptotically) the best performance that any linear code (not necessarily binary) can achieve but also are numerically stable against the inevitable rounding errors in practice. We then develop a low-complexity algorithm for decoding Reed-Muller (RM) codes over erasure channels. Our decoder only involves additions, subtractions, and inversion of relatively small matrices of dimensions at most $\log n+1$ , and enables coded computation over real-valued data. Extensive numerical analysis of the fundamental results as well as RM- and polar-coded computing schemes demonstrate the excellence of the RM-coded computation in achieving close-to-optimal performance while having a low-complexity decoding and explicit construction. The proposed framework in this paper enables efficient designs of distributed computing systems given the rich literature in the channel coding theory.

We propose two coding schemes for distributed matrix multiplication in the presence of stragglers. These coding schemes are adaptations of Luby Transform (LT) codes and Raptor codes to distributed matrix multiplication and are termed Factored LT (FLT) codes and Factored Raptor (FRT) codes. We show that all nodes in the Tanner graph of a randomly sampled code have a tree-like neighborhood with high probability. This ensures that the density evolution analysis gives a reasonable estimate of the average recovery threshold of FLT codes. The recovery threshold of the proposed FLT codes is asymptotically optimal when the output degree distribution is Soliton. Empirically, we show that FRT codes have an excellent recovery threshold while the number of worker nodes is moderately large. In addition, using Azuma–Hoeffding inequality, we derive concentration results to show that the recovery threshold of a randomly chosen FLT code is close to the ensemble average. FLT and FRT codes have better recovery thresholds when compared to Product codes and they are expected to have better numerical stability when compared to Polynomial codes, while they can also be decoded with a low-complexity decoding algorithm. Finally, the proposed codes are better matched to the practically important case of sparse matrix-matrix multiplication as compared to many previous schemes.

We consider the problem of secure distributed matrix multiplication (SDMM) in which a user wishes to compute the product of two matrices with the assistance of honest but curious servers. We construct polynomial codes for SDMM by studying a recently introduced combinatorial tool called the degree table. For a fixed partitioning, minimizing the total communication cost of a polynomial code for SDMM is equivalent to minimizing $N$ , the number of distinct elements in the corresponding degree table. We propose new constructions of degree tables with a low number of distinct elements. These new constructions lead to a general family of polynomial codes for SDMM, which we call $\mathsf {GASP}_{r}$ (Gap Additive Secure Polynomial codes) parameterized by an integer $r$ . $\mathsf {GASP}_{r}$ outperforms all previously known polynomial codes for SDMM under an outer product partitioning. We also present lower bounds on $N$ and prove the optimality or asymptotic optimality of our constructions for certain regimes. Moreover, we formulate the construction of optimal degree tables as an integer linear program and use it to prove the optimality of $\mathsf {GASP}_{r}$ for all the system parameters that we were able to test.

We consider distributed computation of a sequence of $J$ gradients $\{\mathbf {g}(0), \ldots,\mathbf {g}(J-1)\}$ . Each worker node computes a fraction of $\mathbf {g}(t)$ in round- $t$ and attempts to communicate the result to a master. Master is required to obtain the full gradient $\mathbf {g}(t)$ by the end of round- $(t+T)$ . The goal here is to finish all the $J$ gradient computations, keeping the cumulative processing time as short as possible. Delayed availability of results from individual workers causes bottlenecks in this setting. These delays can be due to factors such as processing delay of workers and packet losses. Gradient coding (GC) framework introduced by Tandon et al. uses coding theoretic techniques to mitigate the effect of delayed responses from workers. In this paper, we primarily target mitigating communication-level delays. In contrast to the classical GC approach which performs coding only across workers ( $T=0$ ), the proposed sequential gradient coding framework is more general, as it allows for coding across workers as well as time. We present a new sequential gradient coding scheme which offers improved resiliency against communication-level delays compared to the GC scheme, without increasing computational load. Our experimental results establish performance improvement offered by the new coding scheme.

Zero-knowledge succinct non-interactive argument of knowledge (zkSNARK) allows a party, known as the prover, to convince another party, known as the verifier, that he knows a private value $v$ , without revealing it, such that $F(u,v)=y$ for some function $F$ and public values $u$ and $y$ . There are various versions of zk-SNARK, among them, Quadratic Arithmetic Program (QAP)-based zk-SNARK has been widely used in practice, especially in Blockchain technology. This is attributed to two desirable features; its fixed-size proof and the very light computation load of the verifier. However, the computation load of the prover in QAP-based zkSNARKs is very heavy, even-though it is designed to be very efficient. This load can be beyond the prover’s computation power to handle, and has to be offloaded to some external servers. In the existing offloading solutions, either (i) the load of computation, offloaded to each sever, is a fraction of the prover’s primary computation (e.g., DZIK), however the servers need to be trusted, (ii) the servers are not required to be trusted, but the computation complexity imposed to each one is the same as the prover’s primary computation (e.g., Trinocchio). In this paper, we present a scheme, which has the benefits of both solutions. In particular, we propose a secure multi-party proof generation algorithm where the prover can delegate its task to $N $ servers, where (i) even if a group of $T \in \mathbb {N}$ servers, $T < N$ , collude, they cannot gain any information about the secret value $v$ , (ii) the computation complexity of each server is less than $1/(N-T)$ of the prover’s primary computation. The design is such that we don’t lose the efficiency of the prover’s algorithm in the process of delegating the tasks to external servers.

We develop a communication-efficient distributed learning algorithm that is robust against Byzantine worker machines. We propose and analyze a distributed gradient-descent algorithm that performs a simple thresholding based on gradient norms to mitigate Byzantine failures. We show the (statistical) error-rate of our algorithm matches that of Yin et al. (2018), which uses more complicated schemes (coordinate-wise median, trimmed mean). Furthermore, for communication efficiency, we consider a generic class of $\delta $ -approximate compressors from Karimireddi et al. (2019) that encompasses sign-based compressors and top- $k$ sparsification. Our algorithm uses compressed gradients and gradient norms for aggregation and Byzantine removal respectively. We establish the statistical error rate for non-convex smooth loss functions. We show that, in certain range of the compression factor $\delta $ , the (order-wise) rate of convergence is not affected by the compression operation. Moreover, we analyze the compressed gradient descent algorithm with error feedback (proposed in Karimireddi et al. 2019) in a distributed setting and in the presence of Byzantine worker machines. We show that exploiting error feedback improves the statistical error rate. Finally, we experimentally validate our results and show good performance in convergence for convex (least-square regression) and non-convex (neural network training) problems.

In this paper, we propose and analyze SQuARM-SGD, a communication-efficient algorithm for decentralized training of large-scale machine learning models over a network. In SQuARM-SGD, each node performs a fixed number of local SGD steps using Nesterov’s momentum and then sends sparsified and quantized updates to its neighbors regulated by a locally computable triggering criterion. We provide convergence guarantees of our algorithm for general (non-convex) and convex smooth objectives, which, to the best of our knowledge, is the first theoretical analysis for compressed decentralized SGD with momentum updates. We show that the convergence rate of SQuARM-SGD matches that of vanilla SGD. We empirically show that including momentum updates in SQuARM-SGD can lead to better test performance than the current state-of-the-art which does not consider momentum updates.

An increasing bottleneck in decentralized optimization is communication. Bigger models and growing datasets mean that decentralization of computation is important and that the amount of information exchanged is quickly growing. While compression techniques have been introduced to cope with the latter, none has considered leveraging the temporal correlations that exist in consecutive vector updates. An important example is distributed momentum-SGD where temporal correlation is enhanced by the low-pass-filtering effect of applying momentum. In this paper we design and analyze compression methods that exploit temporal correlation in systems both with and without error-feedback. Experiments with the ImageNet dataset demonstrate that our proposed methods offer significant reduction in the rate of communication at only a negligible increase in computation complexity. We further analyze the convergence of SGD when compression is applied with error-feedback. In the literature, convergence guarantees are developed only for compressors that provide error-bounds point-wise, i.e., for each input to the compressor. In contrast, many important codes (e.g., rate-distortion codes) provide error-bounds only in expectation and thus provide a more general guarantee. In this paper we prove the convergence of SGD under an expected error assumption by establishing a bound for the minimum gradient norm.

We consider machine learning applications that train a model by leveraging data distributed over a trusted network, where communication constraints can create a performance bottleneck. A number of recent approaches propose to overcome this bottleneck through compression of gradient updates. However, as models become larger, so does the size of the gradient updates. In this paper, we propose an alternate approach to learn from distributed data that quantizes data instead of gradients, and can support learning over applications where the size of gradient updates is prohibitive. Our approach leverages the dependency of the computed gradient on data samples, which lie in a much smaller space in order to perform the quantization in the smaller dimension data space. At the cost of an extra gradient computation, the gradient estimate can be refined by conveying the difference between the gradient at the quantized data point and the original gradient using a small number of bits. Lastly, in order to save communication, our approach adds a layer that decides whether to transmit a quantized data sample or not based on its importance for learning. We analyze the convergence of the proposed approach for smooth convex and non-convex objective functions and show that we can achieve order optimal convergence rates with communication that mostly depends on the data rather than the model (gradient) dimension. We use our proposed algorithm to train ResNet models on the CIFAR-10 and ImageNet datasets, and show that we can achieve an order of magnitude savings over gradient compression methods. These communication savings come at the cost of increasing computation at the learning agent, and thus our approach is beneficial in scenarios where communication load is the main problem.

Gradient coding allows a master node to derive the aggregate of the partial gradients, calculated by some worker nodes over the local data sets, with minimum communication cost, and in the presence of stragglers. In this paper, for gradient coding with linear encoding, we characterize the optimum communication cost for heterogeneous distributed systems with arbitrary data placement, with $s \in \mathbb {N}$ stragglers and $a \in \mathbb {N}$ adversarial nodes. In particular, we show that the optimum communication cost, normalized by the size of the gradient vectors, is equal to $(r-s-2a)^{-1}$ , where $r \in \mathbb {N}$ is the minimum number that a data partition is replicated. In other words, the communication cost is determined by the data partition with the minimum replication, irrespective of the structure of the placement. The proposed achievable scheme also allows us to target the computation of a polynomial function of the aggregated gradient matrix. It also allows us to borrow some ideas from approximation computing and propose an approximate gradient coding scheme for the cases when the repetition in data placement is smaller than what is needed to meet the restriction imposed on communication cost or when the number of stragglers appears to be more than the presumed value in the system design.

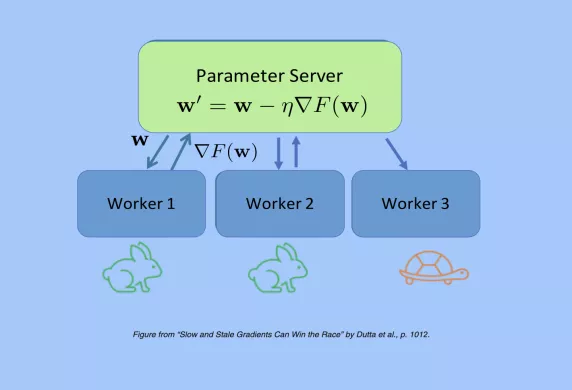
Distributed Stochastic Gradient Descent (SGD) when run in a synchronous manner, suffers from delays in runtime as it waits for the slowest workers (stragglers). Asynchronous methods can alleviate stragglers, but cause gradient staleness that can adversely affect the convergence error. In this work, we present a novel theoretical characterization of the speedup offered by asynchronous methods by analyzing the trade-off between the error in the trained model and the actual training runtime (wallclock time). The main novelty in our work is that our runtime analysis considers random straggling delays, which helps us design and compare distributed SGD algorithms that strike a balance between straggling and staleness. We also provide a new error convergence analysis of asynchronous SGD variants without bounded or exponential delay assumptions. Finally, based on our theoretical characterization of the error-runtime trade-off, we propose a method of gradually varying synchronicity in distributed SGD and demonstrate its performance on the CIFAR10 dataset.

The emerging large-scale and data-hungry algorithms require the computations to be delegated from a central server to several worker nodes. One major challenge in the distributed computations is to tackle delays and failures caused by the stragglers. To address this challenge, introducing efficient amount of redundant computations via distributed coded computation has received significant attention. Recent approaches in this area have mainly focused on introducing minimum computational redundancies to tolerate certain number of stragglers. To the best of our knowledge, the current literature lacks a unified end-to-end design in a heterogeneous setting where the workers can vary in their computation and communication capabilities. The contribution of this paper is to devise a novel framework for joint scheduling-coding, in a setting where the workers and the arrival of stream computational jobs are based on stochastic models. In our initial joint scheme, we propose a systematic framework that illustrates how to select a set of workers and how to split the computational load among the selected workers based on their differences in order to minimize the average in-order job execution delay. Through simulations, we demonstrate that the performance of our framework is dramatically better than the performance of naive method that splits the computational load uniformly among the workers, and it is close to the ideal performance.

Using networks as a means of computing can reduce the communication flow over networks. We propose to distribute the computation load in stationary networks and formulate a flow-based delay minimization problem that jointly captures the costs of communications and computation. We exploit the distributed compression scheme of Slepian-Wolf that is applicable under any protocol information. We introduce the notion of entropic surjectivity as a measure of function’s sparsity and to understand the limits of functional compression for computation. We leverage Little’s law for stationary systems to provide a connection between surjectivity and the computation processing factor that reflects the proportion of flow that requires communications. This connection gives us an understanding of how much a node (in isolation) should compute to communicate the desired function within the network. Our results suggest that to effectively compute different function classes with different surjectivities, the networks can be restructured with the transition probabilities being tailored for functions, i.e., task-based link reservations, which can enable mixing versus separately processing of a diverse function class. We numerically evaluate our technique for search, MapReduce, and classification functions, and infer how sensitive the processing factor to the surjectivity of each computation task is.

In this paper, we study the problem of distributed multi-user secret sharing, including a trusted master node, $N\in \mathbb {N}$ storage nodes, and $K$ users, where each user has access to the contents of a subset of storage nodes. Each user has an independent secret message with certain rate, defined as the size of the message normalized by the size of a storage node. Having access to the secret messages, the trusted master node places encoded shares in the storage nodes, such that (i) each user can recover its own message from the content of the storage nodes that it has access to, (ii) each user cannot gain any information about the message of any other user. We characterize the capacity region of the distributed multi-user secret sharing, defined as the set of all achievable rate tuples, subject to the correctness and privacy constraints. In the achievable scheme, for each user, the master node forms a polynomial with the degree equal to the number of its accessible storage nodes minus one, where the value of this polynomial at certain points are stored as the encoded shares. The message of that user is embedded in some of the coefficients of the polynomial. The remaining coefficients are determined such that the content of each storage node serves as the encoded shares for all users that have access to that storage node.

An error in the proof of the data-dependent tail bounds on the generalization error presented in Hellström and Durisi (2020) is identified, and a correction is proposed. Furthermore, we note that the absolute continuity requirements in Hellström and Durisi (2020) need to be strengthened to avoid measurability issues.