Information theory, starting with Shannon’s groundbreaking work, has fundamentally shaped the way communication systems are designed and operated. Information theoretic principles form the underpinnings of modern communication networks. This issue explores how new advances in information theory can impact future communication systems. Several papers address issues at the heart of next generation wireless and wired networks: Multiple access, including access by a massive number of devices, multi-hop, large antenna arrays, communication security, and timeliness of information. Others consider new applications such as joint communication and sensing, communication for learning and inference, wireless imaging, and new storage mediums such as DNA, thereby providing the information theoretic foundations of modalities beyond human-to-human communications.

Understanding the fundamental limits of technologies enabling future wireless communication systems is essential for their efficient state-of-the-art design. A prominent technology of major interest in this framework is non-orthogonal multiple access (NOMA). In this paper, we derive an explicit rigorous closed-form analytical expression for the optimum spectral efficiency, in the large-system limit, of regular sparse (code-domain) NOMA, along with a closed-form formulation for the limiting spectral density of the underlying input covariance matrix. Sparse NOMA is an attractive and popular instantiation of NOMA, and its ‘regular’ variant corresponds to the case where only a fixed and finite number of orthogonal multiple-access resources are allocated to any designated user, and vice versa. Interestingly, the well-known Verdú-Shamai formula for (dense) randomly-spread code-division multiple access (RS-CDMA) turns out to coincide with the limit of the derived expression, when the number of orthogonal resources per user grows large. Furthermore, regular sparse NOMA is rigorously shown to be spectrally more efficient than RS-CDMA (viz. dense NOMA) across the entire system load range. Therefore, regular sparse NOMA may serve as an appealing means for reducing the throughput gap to orthogonal transmission in the underloaded regime, and to the ultimate Cover-Wyner bound for massive access overloaded systems. The spectral efficiency is also derived in closed form for the sub-optimal linear minimum-mean-square-error (LMMSE) receiver, which again extends the corresponding Verdú-Shamai LMMSE formula to the case of regular sparse NOMA.

This paper considers the Gaussian multiple-access channel in the asymptotic regime where the number of users grows linearly with the code length. We propose efficient coding schemes based on random linear models with approximate message passing (AMP) decoding and derive the asymptotic error rate achieved for a given user density, user payload (in bits), and user energy. The tradeoff between energy-per-bit and achievable user density (for a fixed user payload and target error rate) is studied. It is demonstrated that in the large system limit, a spatially coupled coding scheme with AMP decoding achieves near-optimal tradeoffs for a wide range of user densities. Furthermore, in the regime where the user payload is large, we also study the tradeoff between energy-per-bit and spectral efficiency and discuss methods to reduce decoding complexity.

This paper considers a single-source single-destination half-duplex $n$ -relay network with arbitrary topology, where the source communicates with the destination through a direct link and with the help of $n$ half-duplex relays. The focus is on the linear deterministic approximation of the Gaussian noise network model. First, sufficient conditions under which operating the network in the $n+1$ energy-efficient states (out of the $2^{ n}$ possible states) is sufficient to achieve the approximate capacity (that is, an additive gap approximation of the Shannon capacity) are characterized. Specifically, these $n+ 1$ energy-efficient states are those in which at most one relay is in transmit mode while the rest of the relays are in receive mode. Under such sufficient network conditions, closed-form expressions for the scheduling and the approximate capacity are provided. Then, a time-block relaying scheme, where at each point in time at most one relay is in transmit mode, is designed. In particular, the designed relaying scheme leverages information flow preservation at each relay to explicitly provide the information that each relay is exclusively responsible to store and forward to the destination. Furthermore, the destination can decode the information bits sent by the source in block $B$ by the end of block $B+1$ , and the proposed scheme is shown to achieve the approximate capacity whenever the sufficient conditions are satisfied. Such features make the designed scheme relevant for practical use.

This paper studies the capacity scaling of non-coherent Single-Input Multiple-Output (SIMO) independent and identically distributed (i.i.d.) Rayleigh block fading channels versus bandwidth ( $B$ ), number of receive antennas ( $N$ ) and coherence block length ( $L$ ). In non-coherent channels (without Channel State Information–CSI) capacity scales as $\Theta (\min (B,\sqrt {NL},N))$ . This is achievable using Pilot-Assisted signaling. Energy Modulation signaling rate scales as $\Theta (\min (B,\sqrt {N}))$ . If $L$ is fixed while $B$ and $N$ grow, the two expressions grow equally and Energy Modulation achieves the capacity scaling. However, Energy Modulation rate does not scale as the capacity with the variable $L$ . The coherent channel capacity with a priori CSI, in turn, scales as $\Theta (\min (B,N))$ . The coherent channel capacity scaling can be fully achieved in non-coherent channels when $L\geq \Theta (N)$ . In summary, the channel coherence block length plays a pivotal role in modulation selection and the capacity gap between coherent and non-coherent channels. Pilot-Assisted signaling outperforms Energy Modulation’s rate scaling versus coherence block length. Only in high mobility scenarios where $L$ is much smaller than the number of antennas ( $L\ll \Theta (\sqrt {N})$ ), Energy Modulation is effective in non-coherent channels.

With the advent of 5G and technologies such as cloud computing, Internet-of-Things (IoT), etc, future communication networks will consist of a large number of heterogeneous devices connected together. A critical aspect will be ensuring that communication is not only fast and reliable, but also resilient to malicious attack. As networks increasingly adopt zero-trust principles in their security frameworks, it is important to consider such attacks from a zero-trust perspective. Motivated by this, we consider the problem of communicating a message reliably across a binary erasure channel (BEC( $q$ )) or a binary symmetric channel (BSC( $q$ )) against an adversary actively injecting additional erasures or flips at the channel’s input. The adversary can corrupt up to a fraction $p$ of the transmitted bits and knows the transmission scheme agreed upon by the communicating terminals. Further, he has the capability to causally snoop in on both the transmitter and the receiver in real time, i.e., if ${\mathbf {x}}=(x_{1},x_{2},\ldots, x_{n})$ and ${\mathbf {y}}=(y_{1},y_{2},\ldots, y_{n})$ denote the transmitted and the received codewords respectively, at each time $k$ , he knows $(x_{1},x_{2},\ldots, x_{k})$ and $(y_{1},y_{2},\ldots, y_{k-1})$ . Using his side-information, the adversary is free to employ any attack that respects his constraint on the number of corruptible bits. We prove an information-theoretic tight capacity characterization as a function of $p$ and $q$ for (i) the erasure adversary with a BEC( $q$ ) and (ii) the bit-flip adversary with a BSC( $q$ ). A unique feature of our models is the compounding of stochastic and adversarial noise sources. Our analysis reveals the worst-case adversarial attacks for both models and proves the existence of coding schemes that achieve rates equal to the capacity for any adversarial attack. In the case of bit-flips, we show that, interestingly, when $p$ is below a certain threshold (that depends on $q$ ), the adversary is no worse than an i.i.d. memory-less noise source.

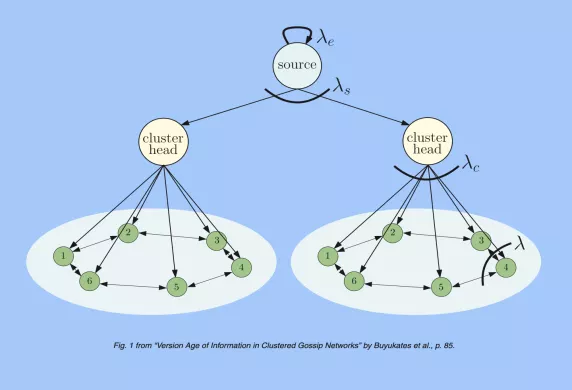
We consider a network consisting of a single source and $n$ receiver nodes that are grouped into equal-sized clusters. Each cluster corresponds to a distinct community such that nodes that belong to different communities cannot exchange information. We use dedicated cluster heads in each cluster to facilitate communication between the source and the nodes within that cluster. Inside clusters, nodes are connected to each other according to a given network topology. Based on the connectivity levels within clusters, each node relays its current stored version of the source update to its neighboring nodes by local gossiping. We consider disconnected, ring, and fully connected network topologies for each cluster. For each of these network topologies, we characterize the average version age at each node and find the average version age scaling as a function of the network size $n$ . Next, by allowing gossiping among the cluster heads, we improve the version age scaling at the receiver nodes. Then, focusing on a ring network topology in each cluster, we introduce hierarchy to the considered clustered gossip network model without using dedicated cluster heads. Finally, we find the version age-optimum cluster sizes as a function of the source, cluster head, and node update rates through numerical evaluations.

This paper considers a multi-source updating system in which a transmitter node powered by energy harvesting (EH) sends status updates about multiple sources of information to a destination, where the freshness of status updates is measured in terms of Age of Information (AoI). The status updates of each source and harvested energy packets are assumed to arrive at the transmitter according to independent Poisson processes, and the service time of each status update is assumed to be exponentially distributed. Further, the transmitter can harvest energy only when its server is idle. Unlike most of the existing queueing-theoretic analyses of AoI that focus on characterizing its average when the transmitter has a reliable energy source and is hence not powered by EH (referred henceforth as a non-EH transmitter), our analysis is focused on understanding the distributional properties of AoI in multi-source systems through the characterization of its moment generating function (MGF). In particular, we use the stochastic hybrid systems (SHS) framework to derive closed-form expressions of the average/MGF of AoI under several queueing disciplines at the transmitter, including non-preemptive and source-agnostic/source-aware preemptive in service strategies. The generality of our results is demonstrated by recovering several existing results as special cases.

We study a basic joint communication and sensing setup from an information theoretic perspective. A transmitter sends an encoded message through a pair of noisy channels connected to a receiver and a sensor. The receiver is interested in decoding the message from its noisy observation. The sensor has access to the message as side information, and instead is interested in estimating an unknown yet fixed binary state of its channel. This basic setup models scenarios where a wireless transceiver broadcasts an information bearing waveform, to be decoded by possibly more than one receiver, and then observes a modulated echo of the waveform from which it wishes to detect an element or object in the environment. We consider binary symmetric and Gaussian settings with multiplicative binary states, and establish the fundamental trade-off between reliable message communication and efficient state detection in these settings. This trade-off is captured by the message communication rate against the state detection error exponent. The results give insights into the benefits of carrying out communication and sensing jointly.

In this paper, we study a distributed learning problem constrained by constant communication bits. Specifically, we consider the distributed hypothesis testing (DHT) problem where two distributed nodes are constrained to transmit a constant number of bits to a central decoder. In such settings, we show that in order to achieve the optimal error exponents, it suffices to consider the empirical distributions of observed data sequences and encode them to the transmission bits. With such a coding strategy, we develop a geometric approach in the distribution spaces and establish an inner bound of error exponent regions. In particular, we show the optimal achievable error exponents and coding schemes for the following cases: (i) both nodes can transmit $\log _{2}3$ bits; (ii) one of the nodes can transmit 1 bit, and the other node is not constrained; (iii) the joint distribution of the nodes are conditionally independent given one hypothesis. Furthermore, we provide several numerical examples for illustrating the theoretical results. Our results provide theoretical guidance for designing practical distributed learning rules, and the developed approach also reveals new potentials for establishing error exponents for DHT with more general communication constraints.

In this paper, we characterize resolution limits for imaging in electromagnetic spectrum where multipath is commonly encountered, e.g., spectrum often used for wireless communication. We analyze a passive system configuration with an aperture of fixed spatial extent sampling fields backscattered from an imaging scene consisting of both line-of-sight (LOS) and non-line-of-sight (NLOS) paths. We characterize the resolution limits using the degrees of freedom (DoF) metric. We make progress towards answering the question: when does multipath offer gains in imaging resolution over LOS-only propagation? Prior theoretical and empirical analysis offer seemingly contradictory answers to this question. On the one hand, prior theoretical analysis suggests that multipath does not improve resolution beyond LOS-only propagation. However, numerical simulations of multipath-exploiting imaging suggest otherwise. We show that the prior results correspond to two extreme operational regimes, under which multipath is equivalent to either LOS-only or NLOS-only propagation. Our DoF analysis unifies prior results, and establishes that: (i) multipath captures the best of both LOS-only and NLOS-only propagation, and (ii) under certain geometric configurations of scatterers, multipath can offer significant resolution gains over LOS-only propagation.

Most DNA sequencing technologies are based on the shotgun paradigm: many short reads are obtained from random unknown locations in the DNA sequence. A fundamental question, in Motahari et al., (2013), is what read length and coverage depth (i.e., the total number of reads) are needed to guarantee reliable sequence reconstruction. Motivated by DNA-based storage, we study the coded version of this problem; i.e., the scenario where the DNA molecule being sequenced is a codeword from a predefined codebook. Our main result is an exact characterization of the capacity of the resulting shotgun sequencing channel as a function of the read length and coverage depth. In particular, our results imply that, while in the uncoded case, $O(n)$ reads of length greater than $2 \log n$ are needed for reliable reconstruction of a length- $n$ binary sequence, in the coded case, only $O(n/\log n)$ reads of length greater than $\log n$ are needed for the capacity to be arbitrarily close to 1.

Coded distributed computing was recently introduced to mitigate the effect of stragglers on distributed computing systems. This paper combines ideas of approximate and coded computing to further accelerate computation. We propose successive approximation coding (SAC) techniques that realize a tradeoff between accuracy and speed, allowing the distributed computing system to produce approximations that increase in accuracy over time. If a sufficient number of compute nodes finish their tasks, SAC exactly recovers the desired computation. We theoretically provide design guidelines for our SAC techniques, and numerically show that SAC achieves a better accuracy-speed tradeoff in comparison with previous methods.

A majority of coded matrix-matrix computation literature has broadly focused in two directions: matrix partitioning for computing a single computation task and batch processing of multiple distinct computation tasks. While these works provide codes with good straggler resilience and fast decoding for their problem spaces, these codes would not be able to take advantage of the natural redundancy of re-using matrices across batch jobs. In this paper, we introduce the Variable Coded Distributed Batch Matrix Multiplication (VCDBMM) problem which tasks a distributed system to perform batch matrix multiplication where matrices are not necessarily distinct among batch jobs. Inspired in part by Cross-Subspace Alignment codes, we develop Flexible Cross-Subspace Alignments (FCSA) codes that are flexible enough to utilize this redundancy. We provide a full characterization of FCSA codes which allow for a wide variety of system complexities including good straggler resilience and fast decoding. We theoretically demonstrate that, under certain practical conditions, FCSA codes are within a factor of 2 of the optimal solution when it comes to straggler resilience. Furthermore, our simulations demonstrate that our codes can achieve even better optimality gaps in practice, even going as low as 1.7.