We study hypergraph clustering in the weighted d-uniform hypergraph stochastic block model (d -WHSBM), where each edge consisting of d nodes from the same community has higher expected weight than the edges consisting of nodes from different communities. We propose a new hypergraph clustering algorithm, called CRTMLE, and provide its performance guarantee under the d -WHSBM for general parameter regimes. We show that the proposed method achieves the order-wise optimal or the best existing results for approximately balanced community sizes. Moreover, our results settle the first recovery guarantees for growing number of clusters of unbalanced sizes. Involving theoretical analysis and empirical results, we demonstrate the robustness of our algorithm against the unbalancedness of community sizes or the presence of outlier nodes.

In this article, we consider a particular data structure consisting of a union of several nested low-rank subspaces with missing data entries. Given the rank of each subspace, we treat the data completion problem, i.e., to estimate the missing entries. Starting from the case of two-dimensional data, i.e., matrices, we show that the union of nested subspaces data structure leads to a structured decomposition U = XY where the factor Y has blocks of zeros that are determined by the rank values. Moreover, for high-dimensional data, i.e., tensors, we show that a similar structured CP decomposition also exists, U = Σl=1r a1l ⊗ a2l ⊗ ··· ⊗ adl, where Ad = [ad1 ···adr] contains blocks of zeros determined by the rank values. Based on such structured decompositions, we develop efficient alternating minimization algorithms for both matrix and tensor completions, by enforcing the above structures in each iteration including the initialization. Compared with naive approaches where either the additional rank constraints are ignored, or data completion is performed part by part, the proposed structured alternating minimization approaches exhibit faster convergence and higher recovery accuracy.

We develop data processing inequalities that describe how Fisher information from statistical samples can scale with the privacy parameter $\varepsilon $ under local differential privacy constraints. These bounds are valid under general conditions on the distribution of the score of the statistical model, and they elucidate under which conditions the dependence on $\varepsilon $ is linear, quadratic, or exponential. We show how these inequalities imply order-optimal lower bounds for private estimation for both the Gaussian location model and discrete distribution estimation for all levels of privacy $\varepsilon >0$ . We further apply these inequalities to sparse Bernoulli models and demonstrate privacy mechanisms and estimators with order-matching squared $\ell ^{2}$ error.

We consider optimization using random projections as a statistical estimation problem, where the squared distance between the predictions from the estimator and the true solution is the error metric. In approximately solving a large-scale least squares problem using Gaussian sketches, we show that the sketched solution has a conditional Gaussian distribution with the true solution as its mean. Firstly, tight worst-case error lower bounds with explicit constants are derived for any estimator using the Gaussian sketch, and the classical sketching is shown to be the optimal unbiased estimator. For biased estimators, the lower bound also incorporates prior knowledge about the true solution. Secondly, we use the James-Stein estimator to derive an improved estimator for the least squares solution using the Gaussian sketch. An upper bound on the expected error of this estimator is derived, which is smaller than the error of the classical Gaussian sketch solution for any given data. The upper and lower bounds match when the SNR of the true solution is known to be small, and the data matrix is well-conditioned. Empirically, this estimator achieves smaller error on simulated and real datasets, and works for other common sketching methods as well.

In this article, we study the problem of non-adaptive group testing, in which one seeks to identify which items are defective given a set of suitably-designed tests whose outcomes indicate whether or not at least one defective item was included in the test. The most widespread recovery criterion seeks to exactly recover the entire defective set, and relaxed criteria such as approximate recovery and list decoding have also been considered. In contrast, we study the fundamental limits of group testing under the significantly relaxed weak recovery criterion, which only seeks to identify a small fraction (e.g., 0.01) of the defective items. Given the near-optimality of i.i.d. Bernoulli testing for exact recovery in sufficiently sparse scaling regimes, it is natural to ask whether this design additionally succeeds with much fewer tests under weak recovery. Our main negative result shows that this is not the case, and in fact, under i.i.d. Bernoulli random testing in the sufficiently sparse regime, an all-or-nothing phenomenon occurs: When the number of tests is slightly below a threshold, weak recovery is impossible, whereas when the number of tests is slightly above the same threshold, high-probability exact recovery is possible. In establishing this result, we additionally prove similar negative results under Bernoulli designs for the weak detection problem (distinguishing between the group testing model vs. completely random outcomes) and the problem of identifying a single item that is definitely defective. On the positive side, we show that all three relaxed recovery criteria can be attained using considerably fewer tests under suitably-chosen non-Bernoulli designs. Thus, our results collectively indicate that when too few tests are available, naively applying i.i.d. Bernoulli testing can lead to catastrophic failure, whereas “cutting one's losses” and adopting a more carefully-chosen design can still succeed in attaining these less stringent criteria.

The problem of distributed testing against independence with variable-length coding is considered when the average and not the maximum communication load is constrained as in previous works. The paper characterizes the optimum type-II error exponent of a single-sensor single-decision center system given a maximum type-I error probability when communication is either over a noise-free rate-R link or over a noisy discrete memoryless channel (DMC) with stop-feedback. Specifically, let E denote the maximum allowed type-I error probability. Then the optimum exponent of the system with a rate-R link under a constraint on the average communication load coincides with the optimum exponent of such a system with a rate R/(1-ε) link under a maximum communication load constraint. A strong converse thus does not hold under an average communication load constraint. A similar observation also holds for testing against independence over DMCs. With variable-length coding and stopfeedback and under an average communication load constraint, the optimum type-II error exponent over a DMC of capacity C equals the optimum exponent under fixed-length coding and a maximum communication load constraint when communication is over a DMC of capacity C/(1 - ε).

Estimating a binary vector from noisy linear measurements is a prototypical problem for MIMO systems. A popular algorithm, called the box-relaxation decoder, estimates the target signal by solving a least squares problem with convex constraints. This article shows that the performance of the algorithm, measured by the number of incorrectly-decoded bits, has a limiting Poisson law. This occurs when the sampling ratio and noise variance, two key parameters of the problem, follow certain scalings as the system dimension grows. Moreover, at a well-defined threshold, the probability of perfect recovery is shown to undergo a phase transition that can be characterized by the Gumbel distribution. Numerical simulations corroborate these theoretical predictions, showing that they match the actual performance of the algorithm even in moderate system dimensions.

We consider rank-one symmetric tensor estimation when the tensor is corrupted by gaussian noise and the spike forming the tensor is a structured signal coming from a generalized linear model. The latter is a mathematically tractable model of a non-trivial hidden lower-dimensional latent structure in a signal. We work in a large dimensional regime with fixed ratio of signal-to-latent space dimensions. Remarkably, in this asymptotic regime, the mutual information between the spike and the observations can be expressed as a finite-dimensional variational problem, and it is possible to deduce the minimum-mean-square-error from its solution. We discuss, on examples, properties of the phase transitions as a function of the signal-to-noise ratio. Typically, the critical signal-to-noise ratio decreases with increasing signal-to-latent space dimensions. We discuss the limit of vanishing ratio of signal-to-latent space dimensions and determine the limiting tensor estimation problem. We also point out similarities and differences with the case of matrices.

This work studies the robust subspace tracking (ST) problem. Robust ST can be simply understood as a (slow) time-varying subspace extension of robust PCA. It assumes that the true data lies in a low-dimensional subspace that is either fixed or changes slowly with time. The goal is to track the changing subspaces over time in the presence of additive sparse outliers and to do this quickly (with a short delay). We introduce a “fast” mini-batch robust ST solution that is provably correct under mild assumptions. Here “fast” means two things: (i) the subspace changes can be detected and the subspaces can be tracked with near-optimal delay, and (ii) the time complexity of doing this is the same as that of simple (non-robust) PCA. Our main result assumes piecewise constant subspaces (needed for identifiability), but we also provide a corollary for the case when there is a little change at each time. A second contribution is a novel non-asymptotic guarantee for PCA in linearly data-dependent noise. An important setting where this is useful is for linearly data dependent noise that is sparse with support that changes enough over time. The analysis of the subspace update step of our proposed robust ST solution uses this result.

This work examines a novel question: how much randomness is needed to achieve local differential privacy (LDP)? A motivating scenario is providing multiple levels of privacy to multiple analysts, either for distribution or for heavy hitter estimation, using the same (randomized) output. We call this setting successive refinement of privacy, as it provides hierarchical access to the raw data with different privacy levels. For example, the same randomized output could enable one analyst to reconstruct the input, while another can only estimate the distribution subject to LDP requirements. This extends the classical Shannon (wiretap) security setting to local differential privacy. We provide (order-wise) tight characterizations of privacy-utility-randomness trade-offs in several cases for distribution estimation, including the standard LDP setting under a randomness constraint. We also provide a non-trivial privacy mechanism for multi-level privacy. Furthermore, we show that we cannot reuse random keys over time while preserving privacy of each user.

Given side information that an Ising tree-structured graphical model is homogeneous and has no external field, we derive the exact asymptotics of learning its structure from independently drawn samples. Our results, which leverage the use of probabilistic tools from the theory of strong large deviations, refine the large deviation (error exponents) results of Tan et al. (2011) and strictly improve those of Bresler and Karzand (2020). In addition, we extend our results to the scenario in which the samples are observed in random noise. In this case, we show that they strictly improve on the recent results of Nikolakakis et al. (2019). Our theoretical results demonstrate keen agreement with experimental results for sample sizes as small as that in the hundreds.

This article studies a high-dimensional inference problem involving the matrix tensor product of random matrices. This problem generalizes a number of contemporary data science problems including the spiked matrix models used in sparse principal component analysis and covariance estimation and the stochastic block model used in network analysis. The main results are single-letter formulas (i.e., analytical expressions that can be approximated numerically) for the mutual information and the minimum mean-squared error (MMSE) in the Bayes optimal setting where the distributions of all random quantities are known. We provide non-asymptotic bounds and show that our formulas describe exactly the leading order terms in the mutual information and MMSE in the high-dimensional regime where the number of rows n and number of columns d scale with d = O(nα) for some α <; 1/20. On the technical side, this article introduces some new techniques for the analysis of high-dimensional matrix-valued signals. Specific contributions include a novel extension of the adaptive interpolation method that uses order-preserving positive semidefinite interpolation paths, and a variance inequality between the overlap and the free energy that is based on continuous-time I-MMSE relations.

We introduce a new general modeling approach for multivariate discrete event data with categorical interacting marks, which we refer to as marked Bernoulli processes. In the proposed model, the probability of an event of a specific category to occur in a location may be influenced by past events at this and other locations. We do not restrict interactions to be positive or decaying over time as it is commonly adopted, allowing us to capture an arbitrary shape of influence from historical events, locations, and events of different categories. In our modeling, prior knowledge is incorporated by allowing general convex constraints on model parameters. We develop two parameter estimation procedures utilizing the constrained Least Squares (LS) and Maximum Likelihood (ML) estimation, which are solved using variational inequalities with monotone operators. We discuss different applications of our approach and illustrate the performance of proposed recovery routines on synthetic examples and a real-world police dataset.

We study the minimax estimation of α-divergences between discrete distributions for integer α ≥ 1, which include the Kullback-Leibler divergence and the χ2-divergences as special examples. Dropping the usual theoretical tricks to acquire independence, we construct the first minimax rate-optimal estimator which does not require any Poissonization, sample splitting, or explicit construction of approximating polynomials. The estimator uses a hybrid approach which solves a problemindependent linear program based on moment matching in the non-smooth regime, and applies a problem-dependent biascorrected plug-in estimator in the smooth regime, with a soft decision boundary between these regimes.

We present a general approach, based on an exponential inequality, to derive bounds on the generalization error of randomized learning algorithms. Using this approach, we provide bounds on the average generalization error as well as bounds on its tail probability, for both the PAC-Bayesian and single-draw scenarios. Specifically, for the case of sub-Gaussian loss functions, we obtain novel bounds that depend on the information density between the training data and the output hypothesis. When suitably weakened, these bounds recover many of the information-theoretic bounds available in the literature. We also extend the proposed exponential-inequality approach to the setting recently introduced by Steinke and Zakynthinou (2020), where the learning algorithm depends on a randomly selected subset of the available training data. For this setup, we present bounds for bounded loss functions in terms of the conditional information density between the output hypothesis and the random variable determining the subset choice, given all training data. Through our approach, we recover the average generalization bound presented by Steinke and Zakynthinou (2020) and extend it to the PAC-Bayesian and single-draw scenarios. For the single-draw scenario, we also obtain novel bounds in terms of the conditional α-mutual information and the conditional maximal leakage.

We consider a finite-armed structured bandit problem in which mean rewards of different arms are known functions of a common hidden parameter 8*. Since we do not place any restrictions on these functions, the problem setting subsumes several previously studied frameworks that assume linear or invertible reward functions. We propose a novel approach to gradually estimate the hidden 8* and use the estimate together with the mean reward functions to substantially reduce exploration of sub-optimal arms. This approach enables us to fundamentally generalize any classical bandit algorithm including UCB and Thompson Sampling to the structured bandit setting. We prove via regret analysis that our proposed UCB-C algorithm (structured bandit versions of UCB) pulls only a subset of the suboptimal arms O(log T) times while the other sub-optimal arms (referred to as non-competitive arms) are pulled O(1) times. As a result, in cases where all sub-optimal arms are non-competitive, which can happen in many practical scenarios, the proposed algorithm achieves bounded regret. We also conduct simulations on the MOVIELENS recommendations dataset to demonstrate the improvement of the proposed algorithms over existing structured bandit algorithms.

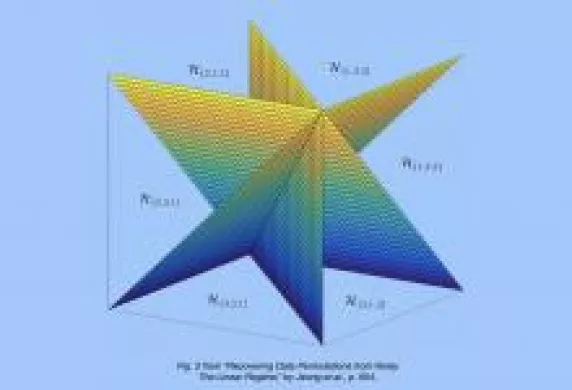
This article considers a noisy data structure recovery problem. The goal is to investigate the following question: given a noisy observation of a permuted data set, according to which permutation was the original data sorted? The focus is on scenarios where data is generated according to an isotropic Gaussian distribution, and the noise is additive Gaussian with an arbitrary covariance matrix. This problem is posed within a hypothesis testing framework. The objective is to study the linear regime in which the optimal decoder has a polynomial complexity in the data size, and it declares the permutation by simply computing a permutation-independent linear function of the noisy observations. The main result of this article is a complete characterization of the linear regime in terms of the noise covariance matrix. Specifically, it is shown that this matrix must have a very flat spectrum with at most three distinct eigenvalues to induce the linear regime. Several practically relevant implications of this result are discussed, and the error probability incurred by the decision criterion in the linear regime is also characterized. A core technical component consists of using linear algebraic and geometric tools, such as Steiner symmetrization.

In the domains of dataset construction and crowdsourcing, a notable challenge is to aggregate labels from a heterogeneous set of labelers, each of whom is potentially an expert in some subset of tasks (and less reliable in others). To reduce costs of hiring human labelers or training automated labeling systems, it is of interest to minimize the number of labelers while ensuring the reliability of the resulting dataset. We model this as the problem of performing K-class classification using the predictions of smaller classifiers, each trained on a subset of [K], and derive bounds on the number of classifiers needed to accurately infer the true class of an unlabeled sample under both adversarial and stochastic assumptions. By exploiting a connection to the classical set cover problem, we produce a near-optimal scheme for designing such configurations of classifiers which recovers the well known one-vs.-one classification approach as a special case. Experiments with the MNIST and CIFAR-10 datasets demonstrate the favorable accuracy (compared to a centralized classifier) of our aggregation scheme applied to classifiers trained on subsets of the data. These results suggest a new way to automatically label data or adapt an existing set of local classifiers to larger-scale multiclass problems.

Fitting multivariate autoregressive (AR) models is fundamental for time-series data analysis in a wide range of applications. This article considers the problem of learning a $p$ -lag multivariate AR model where each time step involves a linear combination of the past $p$ states followed by a probabilistic, possibly nonlinear, mapping to the next state. The problem is to learn the linear connectivity tensor from observations of the states. We focus on the sparse setting, which arises in applications with a limited number of direct connections between variables. For such problems, $\ell _{1}$ -regularized maximum likelihood estimation (or M-estimation more generally) is often straightforward to apply and works well in practice. However, the analysis of such methods is difficult due to the feedback in the state dynamic and the presence of nonlinearities, especially when the underlying process is non-Gaussian. Our main result provides a bound on the mean-squared error of the estimated connectivity tensor as a function of the sparsity and the number of samples, for a class of discrete multivariate AR models, in the high-dimensional regime. Importantly, the bound indicates that, with sufficient sparsity, consistent estimation is possible in cases where the number of samples is significantly less than the total number of parameters.

The large communication cost for exchanging gradients between different nodes significantly limits the scalability of distributed training for large-scale learning models. Motivated by this observation, there has been significant recent interest in techniques that reduce the communication cost of distributed Stochastic Gradient Descent (SGD), with gradient sparsification techniques such as top-k and random-k shown to be particularly effective. The same observation has also motivated a separate line of work in distributed statistical estimation theory focusing on the impact of communication constraints on the estimation efficiency of different statistical models. The primary goal of this paper is to connect these two research lines and demonstrate how statistical estimation models and their analysis can lead to new insights in the design of communication-efficient training techniques. We propose a simple statistical estimation model for the stochastic gradients which captures the sparsity and skewness of their distribution. The statistically optimal communication scheme arising from the analysis of this model leads to a new sparsification technique for SGD, which concatenates random-k and top-k, considered separately in the prior literature. We show through extensive experiments on both image and language domains with CIFAR-10, ImageNet, and Penn Treebank datasets that the concatenated application of these two sparsification methods consistently and significantly outperforms either method applied alone.

Mixed graphical models are widely implemented to capture interactions among different types of variables. To simultaneously learn the topology of multiple mixed graphical models and encourage common structure, people have developed a variational maximum likelihood inference approach, which takes advantage of the log-determinant relaxation. In this article, we further improve the computational efficiency of this method by exploiting the block diagonal structure of the solution. We present a simple necessary and sufficient condition to identify the connected components in the solution, so as to determine the block diagonal structure. Then, utilizing the idea of “divide-and-conquer”, we are able to adapt the joint structural inference problem for multiple related large sparse networks. We illustrate the merits of the proposed algorithm via experimental comparisons in computational speed.

Datasets from the fields of bioinformatics, chemometrics, and face recognition are typically characterized by small samples of high-dimensional data. Among the many variants of linear discriminant analysis that have been proposed in order to rectify the issues associated with classification in such a setting, the classifier in (Durrant and Kabán, 2013), composed of an ensemble of randomly projected linear discriminants, seems especially promising; it is computationally efficient and, with the optimal projection dimension parameter setting, is competitive with the state-of-the-art. In this work, we seek to further understand the behavior of this classifier through asymptotic analysis. Under the assumption of a growth regime in which the dataset and projection dimensions grow at constant rates to each other, we use random matrix theory to derive asymptotic misclassification probabilities showing the effect of the ensemble as a regularization of the data sample covariance matrix. The asymptotic errors further help to identify situations in which the ensemble offers a performance advantage. We also develop a consistent estimator of the misclassification probability as an alternative to the computationally-costly cross-validation estimator, which is conventionally used for parameter tuning. Finally, we demonstrate the use of our estimator for tuning the projection dimension on both real and synthetic data.